
2014학년도 수학 가형 29번 기하 문제입니다.
제가 봤던 수능에서 나온 문제인데 개인적으로 30번보다 여기서 시간을 많이 잡아먹었던 기억이 있네요..😂
$\overrightarrow{PQ}$벡터를 $(a, b, c)$ 문자로 설정하고 풀려고 하니깐 답도 없어서 다른 방향으로 풀어야겠다고 중간에 풀이 방향을 바꾸는 바람에.. 다른 문제 검산할 시간이 없어서 힘들었었어요..
아무튼 tmi는 이쯤 하고, 풀이를 시작할게요ㅎㅎ
문제 풀이 편의상 $y=4$ 평면을 $\alpha$평면, $y + \sqrt{3} z + 8 = 0$ 평면을 $\beta$평면이라고 칭하겠습니다.
다음과 같은 과정으로 문제 풀이를 진행할게요.
🔑1 : $2 \left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_1 Q_1} \right|^2 - \left| \overrightarrow{P_2 Q_2} \right|^2$ 를 $ (\left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_1 Q_1} \right|^2) + ( \left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_2 Q_2} \right|^2)$로 바꾸면서 식의 의미 알아내기
🔑2 : 공간에서 구 $x^2 + y^2 + z^2 = 4$와 $\alpha$평면, $\beta$평면의 위치 관계 알아보기.
🔑3 : $ \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_1) + \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_2)$의 값은, $\overrightarrow{PQ}$가 $\gamma$평면 상에 있을때 최대가 됨을 밝히기.
(2가지 설명)
🔑4 : $2 \left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_1 Q_1} \right|^2 - \left| \overrightarrow{P_2 Q_2} \right|^2$의 최댓값(문제 정답) 구하기
그러면 시작하겠습니다!
🔑1
$2 \left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_1 Q_1} \right|^2 - \left| \overrightarrow{P_2 Q_2} \right|^2$ 를 $ (\left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_1 Q_1} \right|^2) + ( \left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_2 Q_2} \right|^2)$로 바꾸면서 식의 의미 알아내기
$2 \left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_1 Q_1} \right|^2 - \left| \overrightarrow{P_2 Q_2} \right|^2$ 를 $ (\left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_1 Q_1} \right|^2) + ( \left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_2 Q_2} \right|^2)$ 식으로 바꾸면,
식의 구성이 $ (\left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_1 Q_1} \right|^2)$과 $( \left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_2 Q_2} \right|^2)$ 두가지 성분의 합임을 알 수 있습니다.
각각이 의미하는 바를 알기 위해, $ (\left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_1 Q_1} \right|^2)$ 부터 의미를 알아보죠.
$\overrightarrow{PQ}$를 $\alpha$평면에 정사영 한 것이 $\overrightarrow{P_1 Q_1}$이 되므로,

다음과 같은 관계로 $ \left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_1 Q_1} \right|^2$이 $ \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_1)$로 변함을 알 수 있습니다.
같은 방법으로 $\overrightarrow{PQ}$를 $\beta$평면에 정사영 한 것이 $\overrightarrow{P_2 Q_2}$ 이고, $\overrightarrow{PQ}$가 $\beta$평면의 법선벡터와 이루는 각을 $\theta_2$라고 한다면,
$ \left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_2 Q_2} \right|^2 = \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_2)$임을 알 수 있습니다.
$$\therefore 2 \left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_1 Q_1} \right|^2 - \left| \overrightarrow{P_2 Q_2} \right|^2 = (\left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_1 Q_1} \right|^2) + ( \left| \overrightarrow{PQ} \right|^2 - \left| \overrightarrow{P_2 Q_2} \right|^2)$$
$$= \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_1) + \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_2)$$
이렇게 식이 바뀌었습니다! $ \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_1) + \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_2)$의 최댓값을 구하는 것으로 바뀌었는데, 지금까지의 정보로 이 식의 최댓값을 바로 구할 수는 없겠죠?ㅎㅎ 이렇게 식이 바뀌고 나니 "아! 이 문제는 이제 삼각함수 합성의 문제구나. 그러면 $\theta_1$과 $\theta_2$를 한 문자로 줄여야 되겠구나. 그러려면 $\theta_1$과 $\theta_2$와의 관계를 밝혀내야겠네."라는 생각을 가지게 되었습니다.
이쯤 하고 다음 단계로 넘어가죠.
🔑2
공간에서 구 $x^2 + y^2 + z^2 = 4$와 $\alpha$평면, $\beta$평면의 위치 관계 알아보기.
이 부분은 사실 기하를 배우신 분이라면 누구나 쉽게 할 수 있겠죠?

구의 중심으로부터 $\alpha$평면, $\beta$평면 까지의 수직 거리가 4로 같고, 두 평면이 이루는 각의 크기가 $\frac{\pi}{3}$임을 이용하여, 구와 평면들의 위치관계를 다음과 같이 그릴 수 있습니다.
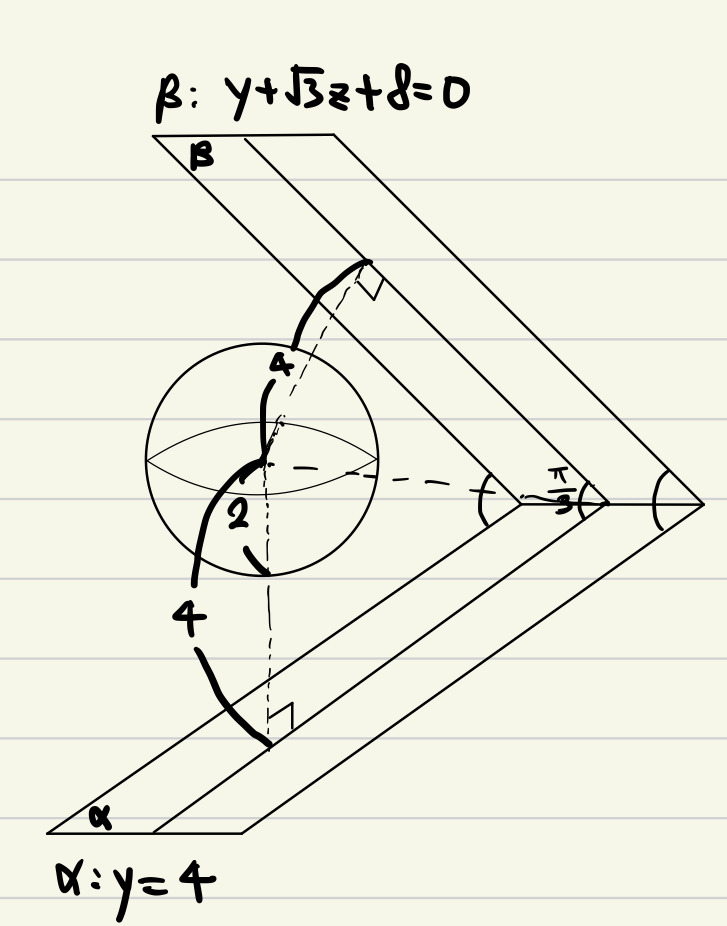
그리고, 문제 풀이 과정 상 반드시 필요한 평면인, $\gamma : x = 0$평면 하나를 추가하겠습니다.
$\gamma$평면의 법선벡터 $(1,0,0)$ 은
$\alpha$, $\beta$평면의 법선벡터인 $(0,1,0)$, $(0,1,\sqrt{3})$과 내적값이 모두 0이므로
$\gamma$평면은 $\alpha$, $\beta$평면과 모두 수직을 이룹니다. 따라서 $\gamma$평면을 추가한 그림을 그리면,

다음 그림과 같고, $\gamma$평면과 $\alpha$, $\beta$평면, 그리고 구 $x^2 + y^2 + z^2 = 4$가 만나서 생기는 저 하늘색 선을 $\gamma$평면에서 바라본다면,
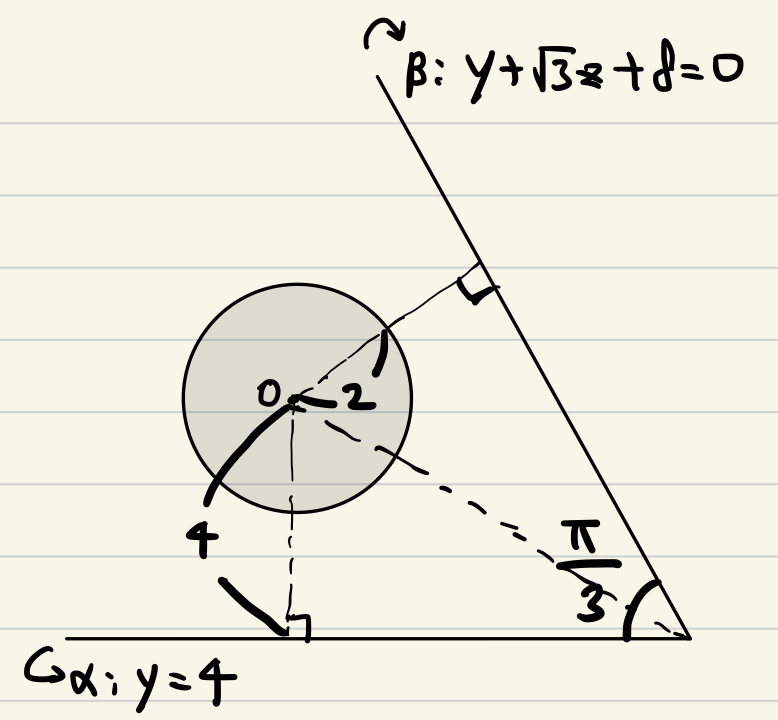
이렇게 되겠죠!
🔑3
$ \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_1) + \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_2)$의 값은,
$\overrightarrow{PQ}$가 $\gamma$평면 상에 있을때 최대가 됨을 밝히기.
(2가지 설명 방법으로 보일 예정입니다)
(tmi : 사실 이 부분에 대한 이해만 확실하다면, 나머지 문제를 푸는 과정이야 $ \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_1) + \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_2)$ 식을 삼각함수 공식을 이용하여 최대값을 구하는 것이라 매우 간단한데, 이 🔑3의 이해를 돕기 위해서 제가 그림을 정말 많이 그렸어요,,, 설명에 어려움이 많아 애를 많이 먹었네요🥲)
먼저 $ \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_1) + \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_2) = \left| \overrightarrow{PQ} \right|^2(cos^2(\theta_1)+cos^2(\theta_2))$의 식이 최대가 되려면, $ \left| \overrightarrow{PQ} \right| = 4$ 여야 하겠죠? 따라서,
$$ \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_1) + \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_2) = \left| \overrightarrow{PQ} \right|^2(cos^2(\theta_1)+cos^2(\theta_2)) = 16(cos^2(\theta_1)+cos^2(\theta_2))$$
가 되고, 여기서 $\theta_1$은 $\alpha$평면의 "법선벡터"와 이루는 각이고, $\theta_2$은 $\beta$평면의 "법선벡터"와 이루는 각이라는 것을 기억해두셔야 합니다!
이 쯤까지 식 정리를 해두고, 이제 본격적으로 $ \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_1) + \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_2)$의 값은, $\overrightarrow{PQ}$가 $\gamma$평면 상에 있을때 최대가 됨을 설명하겠습니다.
◈설명 1. 수식을 이용하여 설명
$\overrightarrow{PQ} = (a,b,c)$로 두었을때,
$a, b, c$는 등식 $a^2 + b^2 + c^2 = 16$을 만족하는 모든 실수의 순서쌍 $(a,b,c)$입니다.
이제 $\overrightarrow{PQ} = (a,b,c)$를 이용하여 $16(cos^2(\theta_1)+cos^2(\theta_2))$의 식을 $b,c$에 관한 식으로 고치겠습니다.

다음과 같은 과정으로,
$$16(cos^2(\theta_1)+cos^2(\theta_2)) = \frac{5b^2 + 2\sqrt{3} bc + 3c^2}{4}$$의 식을 얻었습니다.
등식 $a^2 + b^2 + c^2 = 16$을 만족하는 모든 실수의 순서쌍 $(a,b,c)$ 에 대하여, 다음 식이 최대가 되기 위해서는, 두가지 조건이 만족되어야 합니다.
** $a = 0$이어야만 합니다.(등식 $a^2 + b^2 + c^2 = 16$에서 실수 $a$의 절댓값이 늘어날 수록, $b$와 $c$의 절댓값이 작아지기 때문에)
** $bc > 0$ 즉, $b$와 $c$의 부호가 같음.
다음과 같은 이유로 $a=0$ 즉, $\overrightarrow{PQ} = (a,b,c)$는 그 $x$성분이 0이어야 합니다. 다른 의미로, $\overrightarrow{PQ}$는 $yz$평면 = $\gamma$평면 상에 있어야 한다는 것을 알 수 있습니다. 또한 $b$와 $c$의 부호가 같으므로, $\overrightarrow{PQ}$는 $yz$평면 상의 제 1사분면 혹은 제 3사분면을 향해야 함을 알 수 있습니다. 이러한 조건을 고려하면 $\overrightarrow{PQ}$는 아래 그림과 같은 형태로 공간 상에 존재해야 합니다.
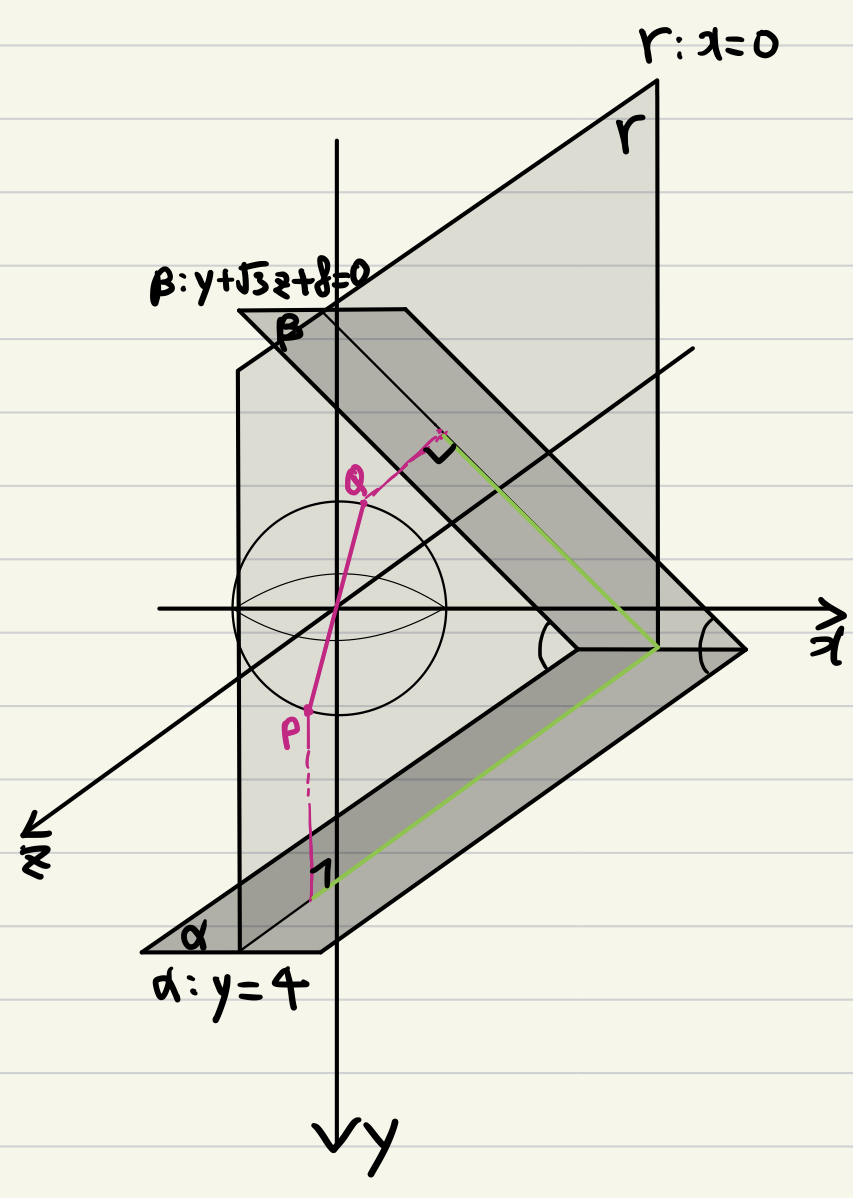
◈설명 2. (이 설명이 좀 더 정확한 설명입니다)
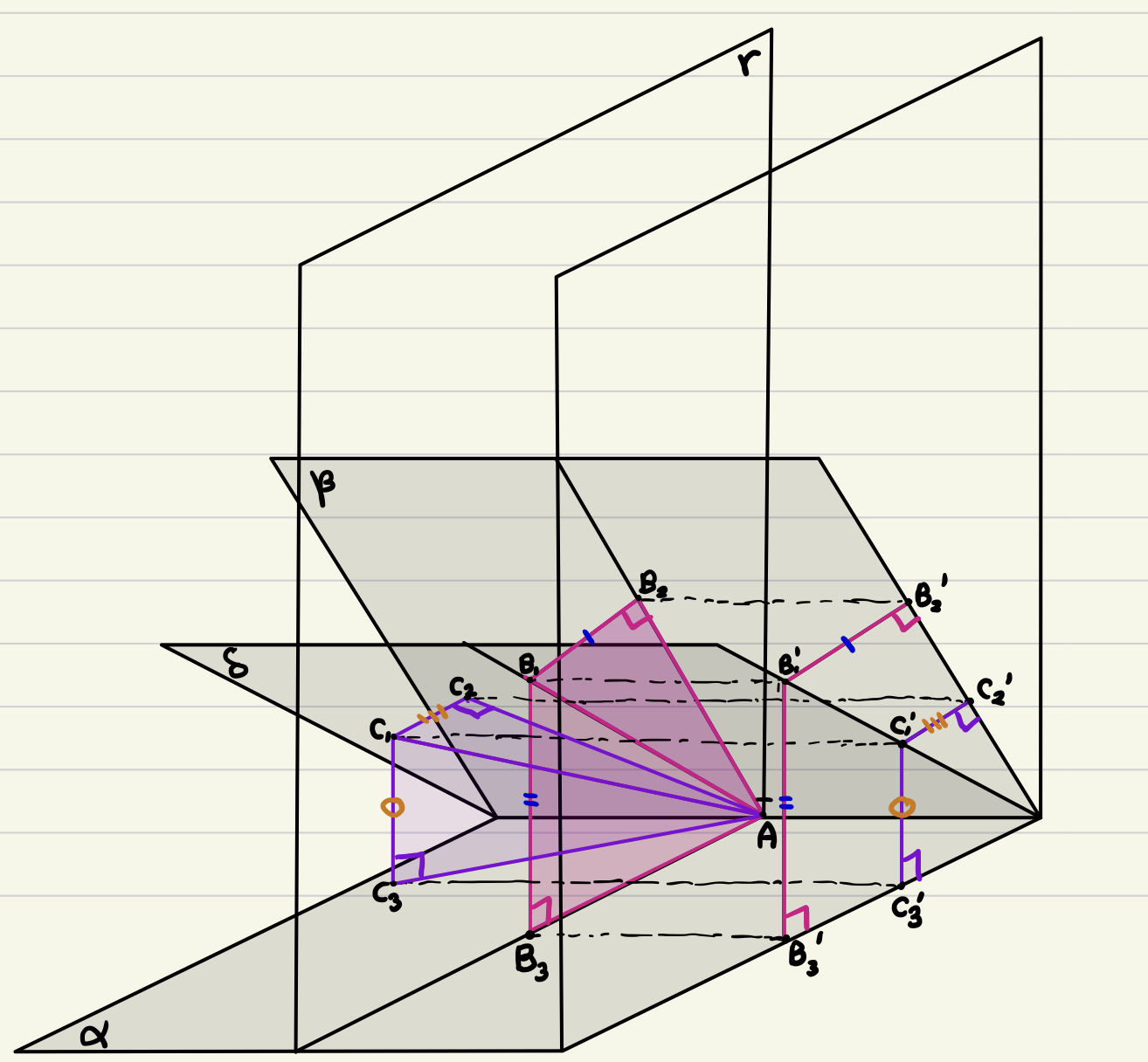
이번엔 $\overrightarrow{PQ}$ 벡터의 시점과 종점 중 한 점을 $\alpha$평면과 $\beta$평면의 교선 위로 평행이동 시킴으로써 생각해보겠습니다.
위 그림을 보았을 때, $\gamma$평면 위의 길이가 4인 임의의 선분 $\overline{AB_1}$라고 하겠습니다.
$B_1$에서 $\alpha$, $\beta$ 평면에 내린 수선의 발을 $B_2$, $B_3$라고 할게요.
그리고 이 선분 $\overline{AB_1}$를 기울였을 때 선분을 $\overline{AC_1}$(얘도 길이가 4겠죠)
$C_1$에서 $\alpha$, $\beta$ 평면에 내린 수선의 발을 $C_2$, $C_3$라고 할게요.
이렇게 그림을 그려놓고 보면 $\gamma$평면 위의 $\overline{AB}$를 양쪽으로 기울였을 때,
(기울임을 엄밀히 정의 하자면, $\alpha$, $\beta$ 평면의 교선을 지나며 $\alpha$평면 과 이루는 각의 크기가 임의의 값 k인 $\delta$ 평면 위의 길이가 4인 선분들 중, $\alpha$, $\beta$ 평면의 교선과 수직인 선분 $\overline{AB_1}$와, 그렇지 않은 $\overline{AC_1}$에 대하여,)
$\overline{B_1 B_2} > \overline{C_1 C_2}$ , $\overline{B_1 B_3} > \overline{C_1 C_3}$가 반드시 성립함을 알 수 있습니다.
즉, $\gamma$평면 위의 $\overline{AB}$를 기울이면 기울일수록 $\overline{B_1 B_2}$와 $\overline{B_1 B_3}$의 길이가 점점 짧아지기 때문에,
$\overline{B_1 B_2}$,$\overline{B_1 B_3}$가 길이가 최대가 되기 위해서 $\overline{AB}$는 $\gamma$평면 상에 놓여 있어야 된다는 뜻입니다.
(왜냐하면 $\overline{AB_1}$을 기울이게 될 수록, 이 선분과 $\alpha$평면, $\beta$ 평면과 이루는 각의 크기가 점점 커지기 때문입니다.
$\overline{AB_1}$가 $\gamma$평면 상에 있을 때 $\theta_1 + \theta_2 = \frac{2}{3} \pi$이고,
$\overline{AB_1}$이 점점 기울어져 $\alpha$, $\beta$ 평면의 교선상에 놓이게 될 때 $\theta_1 + \theta_2 = \pi$가 됩니다.)
이 점 $A$, $B$를 각각 $P$, $Q$로 대체 시켜 생각 해보면,
$\overline{B_1 B_3} = \left| \overrightarrow{PQ} \right| cos(\theta_1)$,
$\overline{B_1 B_2} = \left| \overrightarrow{PQ} \right| cos(\theta_2)$임을 알 수 있고,
이와 같은 과정으로 $\left| \overrightarrow{PQ} \right|^2 cos^2(\theta_1) + \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_2)$가 최대가 되기 위해서 $\overrightarrow{PQ}$는 $\gamma$평면 상에 놓여 있어야 하며, 이때, $$\theta_1 + \theta_2 = \frac{2}{3} \pi$$
임이 밝혀졌습니다.
🔑4(마지막!)
$\theta_1 + \theta_2 = \frac{2}{3} \pi$임을 이용하여
$\left| \overrightarrow{PQ} \right|^2 cos^2(\theta_1) + \left| \overrightarrow{PQ} \right|^2 cos^2(\theta_2)$의 최댓값 구하기
$cos^2(\frac{\alpha}{2}) = \frac{1+cos(\alpha)}{2}$임을 이용하여 다음과 같이 정리하죠

이와 같은 과정으로 문제의 답은 24임이 밝혀졌습니다.
사실 직관적으로 $\overrightarrow{PQ}$가 $yz$평면 상에 있을 때 최대가 됨을 직관적으로 파악하면 문제 푸는 과정 자체는 되게 쉬웠던 문제이지만, $yz$평면 상에 있어야 하는 이유를 밝혀내기가 좀 까다로웠던 문제입니다.
문제 풀이과정에서 쓰이는 삼각함수 공식은 이제 미적분에서 배우게 되고, 이 문제는 엄연히 기하 문제이기 때문에 미적분과 기하를 둘 다 알아야지만 풀 수 있는 문제기에, 더 이상 이런 문제 유형은 출제되지 않겠지만, 충분히 흥미로운 문제여서 한번 쯤 풀어보시면 좋을 문제입니다.
이상으로 14학년도 수능 가형 29번 문제 풀이를 마치겠습니다👏
'고 3 (수능)' 카테고리의 다른 글
| (교육청 기출) 2018년 7월 수학 가형 21번 (0) | 2021.08.04 |
|---|---|
| (평가원 기출) 2018학년도 6월 모의고사 수학 가형 21번 (0) | 2021.08.02 |
| (수능 기출)2018학년도 수능 수학 가형 30번 (0) | 2021.08.02 |
| (수능 기출) 2019학년도 수능 수학 가형 30번 (0) | 2021.07.16 |